Trường Hợp Tam Giác Bằng Nhau là một trong những kiến thức nền tảng quan trọng trong hình học phẳng. Bài viết này sẽ cùng bạn khám phá chi tiết về các trường hợp tam giác bằng nhau, từ định nghĩa, phân loại đến ứng dụng thực tiễn, gắn liền với hành trình học tập tại THPT Gia Định.
Các Trường Hợp Tam Giác Bằng Nhau: Nền Tảng Của Hình Học
Các trường hợp tam giác bằng nhau là điều kiện cần và đủ để hai tam giác được coi là bằng nhau. Điều này có nghĩa là nếu hai tam giác thỏa mãn một trong các trường hợp này, thì chúng có tất cả các cạnh và góc tương ứng bằng nhau. Ngược lại, nếu tất cả các cạnh và góc tương ứng của hai tam giác bằng nhau, thì chúng thỏa mãn ít nhất một trong các trường hợp tam giác bằng nhau. Việc nắm vững kiến thức này không chỉ giúp học sinh THPT Gia Định đạt điểm cao trong các bài kiểm tra mà còn rèn luyện tư duy logic và khả năng phân tích, giải quyết vấn đề. các trường hợp tam giác bằng nhau
Trường Hợp Cạnh – Cạnh – Cạnh (c.c.c)
Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau. Đây là trường hợp bằng nhau cơ bản nhất và dễ hình dung nhất.
Trường Hợp Cạnh – Góc – Cạnh (c.g.c)
Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau. Lưu ý, góc phải nằm giữa hai cạnh đã cho.
Trường Hợp Góc – Cạnh – Góc (g.c.g)
Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
Trường Hợp Tam Giác Bằng Nhau Của Tam Giác Vuông
Đối với tam giác vuông, ngoài ba trường hợp cơ bản, chúng ta còn có thêm hai trường hợp đặc biệt. các trường hợp bằng nhau của hai tam giác vuông
Trường Hợp Cạnh Huyền – Cạnh Góc Vuông
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Trường Hợp Cạnh Huyền – Góc Nhọn
Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Ứng Dụng Trường Hợp Tam Giác Bằng Nhau Trong Thực Tiễn
Tại THPT Gia Định, học sinh không chỉ học lý thuyết suông mà còn được áp dụng kiến thức vào thực tế thông qua các bài tập thực hành, dự án nghiên cứu khoa học. Ví dụ, trường hợp bằng nhau của tam giác có thể được ứng dụng để đo khoảng cách giữa hai điểm mà ta không thể đo trực tiếp, tính toán độ cao của một tòa nhà, hoặc thiết kế các công trình kiến trúc. trường hợp 2 tam giác bằng nhau
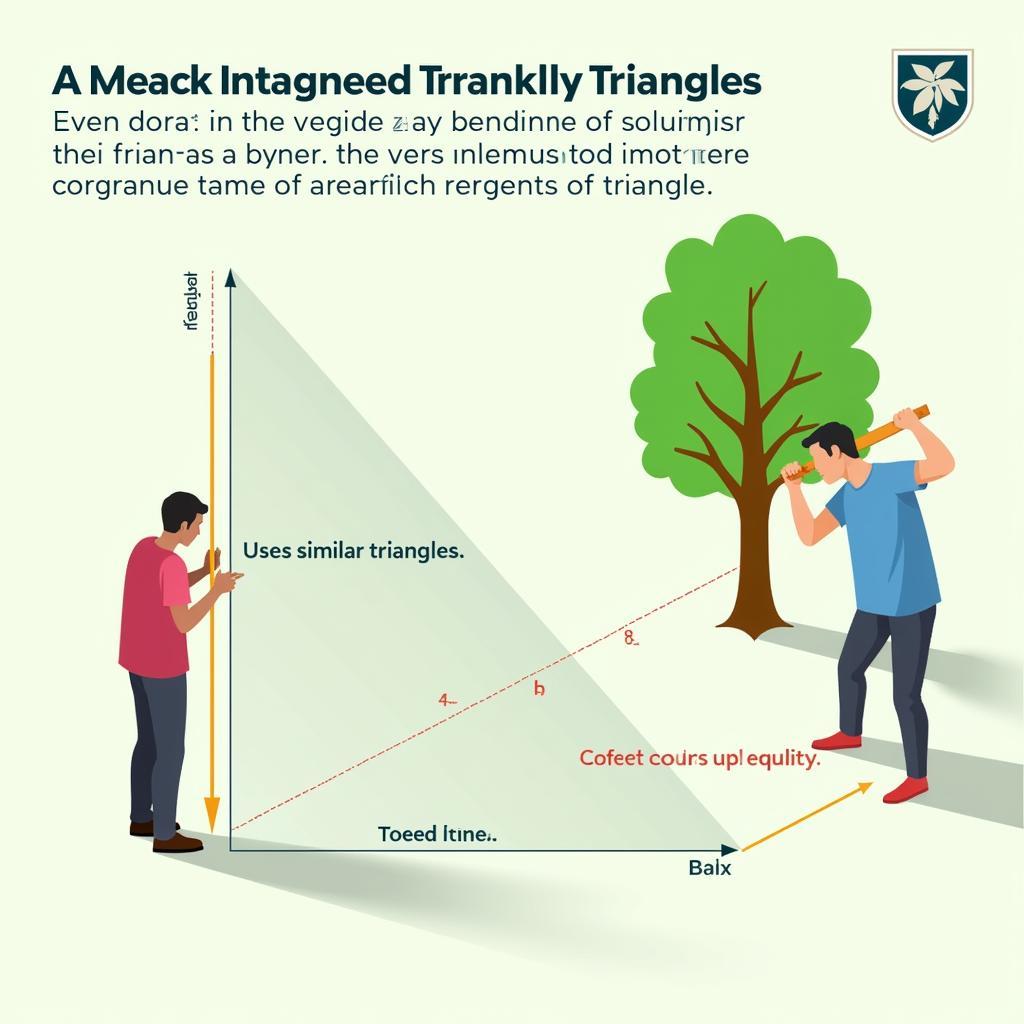Hình ảnh minh họa ứng dụng thực tế của trường hợp tam giác bằng nhau, ví dụ như đo chiều cao của một cái cây bằng cách sử dụng hai tam giác đồng dạng
Kết luận
Trường hợp tam giác bằng nhau là một phần kiến thức quan trọng trong chương trình toán học tại THPT Gia Định. Hiểu rõ và vận dụng thành thạo các trường hợp bằng nhau của tam giác thường sẽ giúp học sinh phát triển tư duy toán học, giải quyết các bài toán hình học phẳng và có nền tảng vững chắc cho việc học tập các kiến thức nâng cao hơn.
Khi cần hỗ trợ hãy liên hệ Số Điện Thoại: 02223831609, Email: [email protected] Hoặc đến địa chỉ: Đ. Nguyễn Văn Cừ, Trang Hạ, Từ Sơn, Bắc Ninh, Việt Nam. Chúng tôi có đội ngũ chăm sóc khách hàng 24/7.
