Khám Phá Bài Tập Các Trường Hợp Bằng Nhau Của Tam Giác Tại THPT Gia Định

Trong hành trình chinh phục tri thức toán học tại THPT Gia Định, các bạn học sinh sẽ được tiếp cận với những kiến thức nền tảng và vô cùng thú vị. Một trong số đó là “Bài Tập Các Trường Hợp Bằng Nhau Của Tam Giác” – chìa khóa mở ra cánh cửa đến với thế giới hình học đầy màu sắc.

Trường Hợp Bằng Nhau Cạnh – Cạnh – Cạnh (c.c.c)

Đây là trường hợp cơ bản và dễ nhận biết nhất. Hai tam giác được gọi là bằng nhau theo trường hợp c.c.c nếu ba cạnh của tam giác này lần lượt bằng ba cạnh của tam giác kia.

Ví dụ, tam giác ABC và tam giác DEF có:

AB = DE
BC = EF
CA = FD

Thì ta kết luận tam giác ABC bằng tam giác DEF (theo trường hợp c.c.c)

Trường Hợp Bằng Nhau Cạnh – Góc – Cạnh (c.g.c)

Hai tam giác bằng nhau theo trường hợp c.g.c nếu hai cạnh và góc xen giữa của tam giác này lần lượt bằng hai cạnh và góc xen giữa của tam giác kia.

Ví dụ, tam giác MNP và tam giác RST có:

MN = RS
góc MNP = góc RST
NP = ST

Thì ta kết luận tam giác MNP bằng tam giác RST (theo trường hợp c.g.c)

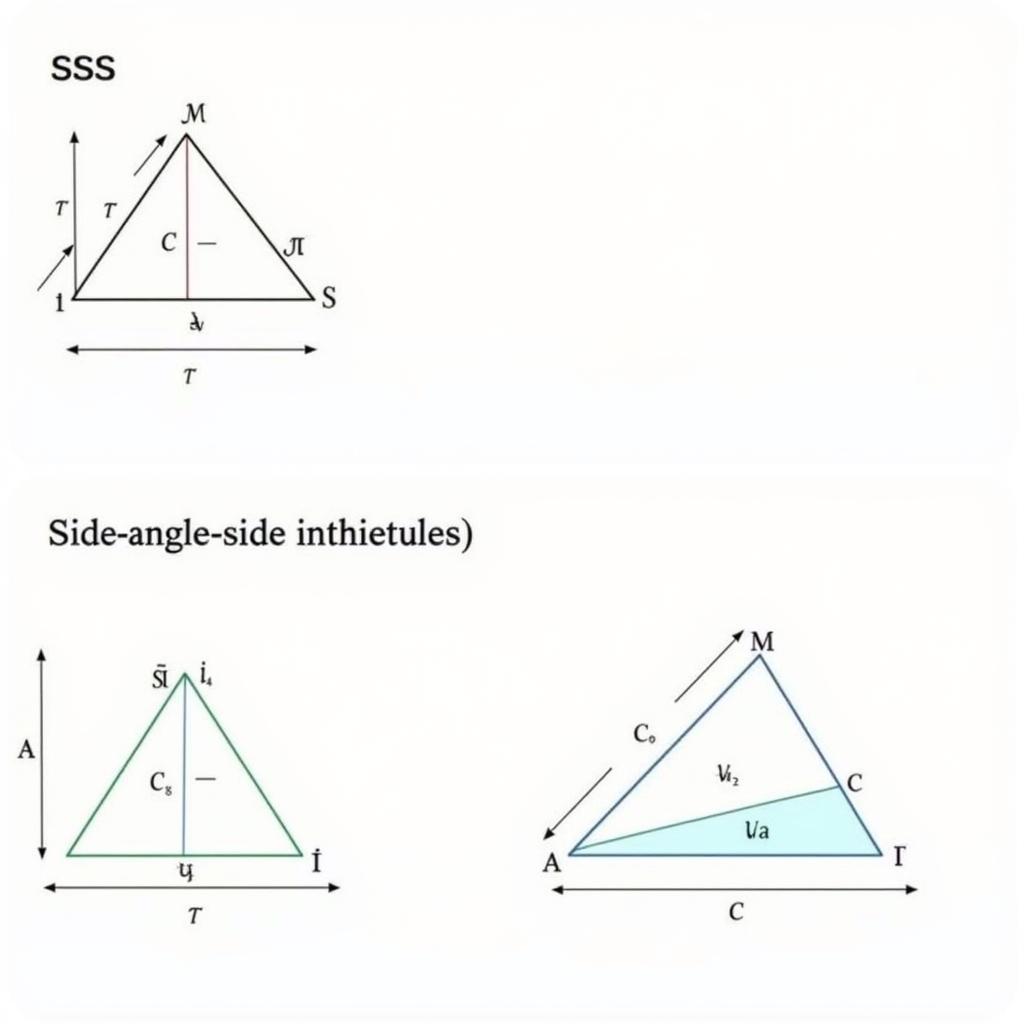Hình minh họa các trường hợp bằng nhau của tam giác, bao gồm trường hợp c.c.c và c.g.c

Trường Hợp Bằng Nhau Góc – Cạnh – Góc (g.c.g)

Hai tam giác bằng nhau theo trường hợp g.c.g nếu một cạnh và hai góc kề của tam giác này lần lượt bằng một cạnh và hai góc kề của tam giác kia.

Ví dụ, tam giác XYZ và tam giác UVW có:

góc XYZ = góc UVW
XY = UV
góc YXZ = góc VWU

Thì ta kết luận tam giác XYZ bằng tam giác UVW (theo trường hợp g.c.g)

Ứng Dụng Của Các Trường Hợp Bằng Nhau Của Tam Giác

Trong toán học: Các trường hợp bằng nhau của tam giác là nền tảng để chứng minh các định lý, tính toán các yếu tố hình học trong tam giác và các hình phức tạp hơn.
Trong thực tiễn: Kiến thức về các trường hợp bằng nhau của tam giác được ứng dụng rộng rãi trong các lĩnh vực như xây dựng, kiến trúc, thiết kế, đo đạc,…

Hình ảnh minh họa ứng dụng thực tiễn của bài tập trường hợp bằng nhau của tam giác trong thiết kế cầu đường

Kết Luận

“Bài tập các trường hợp bằng nhau của tam giác” là một phần kiến thức quan trọng, giúp học sinh THPT Gia Định phát triển tư duy logic, khả năng phân tích và giải quyết vấn đề.