Trường Hợp 2 Tam Giác Bằng Nhau là một kiến thức nền tảng quan trọng trong hình học, giúp học sinh THPT Gia Định giải quyết nhiều bài toán phức tạp. Bài viết này sẽ đi sâu vào tìm hiểu trường hợp bằng nhau thứ hai của hai tam giác, cùng những ứng dụng thực tiễn thú vị của nó trong cuộc sống. tả quang cảnh trường em vào buổi sáng
Trường Hợp Bằng Nhau Thứ Hai: Cạnh – Góc – Cạnh (c-g-c)
Trường hợp bằng nhau thứ hai (c-g-c) phát biểu rằng hai tam giác bằng nhau nếu chúng có hai cạnh tương ứng bằng nhau và góc xen giữa hai cạnh đó cũng bằng nhau. Đây là một trong những trường hợp bằng nhau cơ bản, được học sinh THPT Gia Định áp dụng thường xuyên trong các bài toán chứng minh hình học.
Điều Kiện Cần và Đủ Để Hai Tam Giác Bằng Nhau Theo Trường Hợp c-g-c
Để chứng minh hai tam giác bằng nhau theo trường hợp c-g-c, ta cần chỉ ra được ba yếu tố sau:
- Hai cạnh tương ứng của hai tam giác bằng nhau.
- Góc xen giữa hai cạnh đó của hai tam giác bằng nhau.
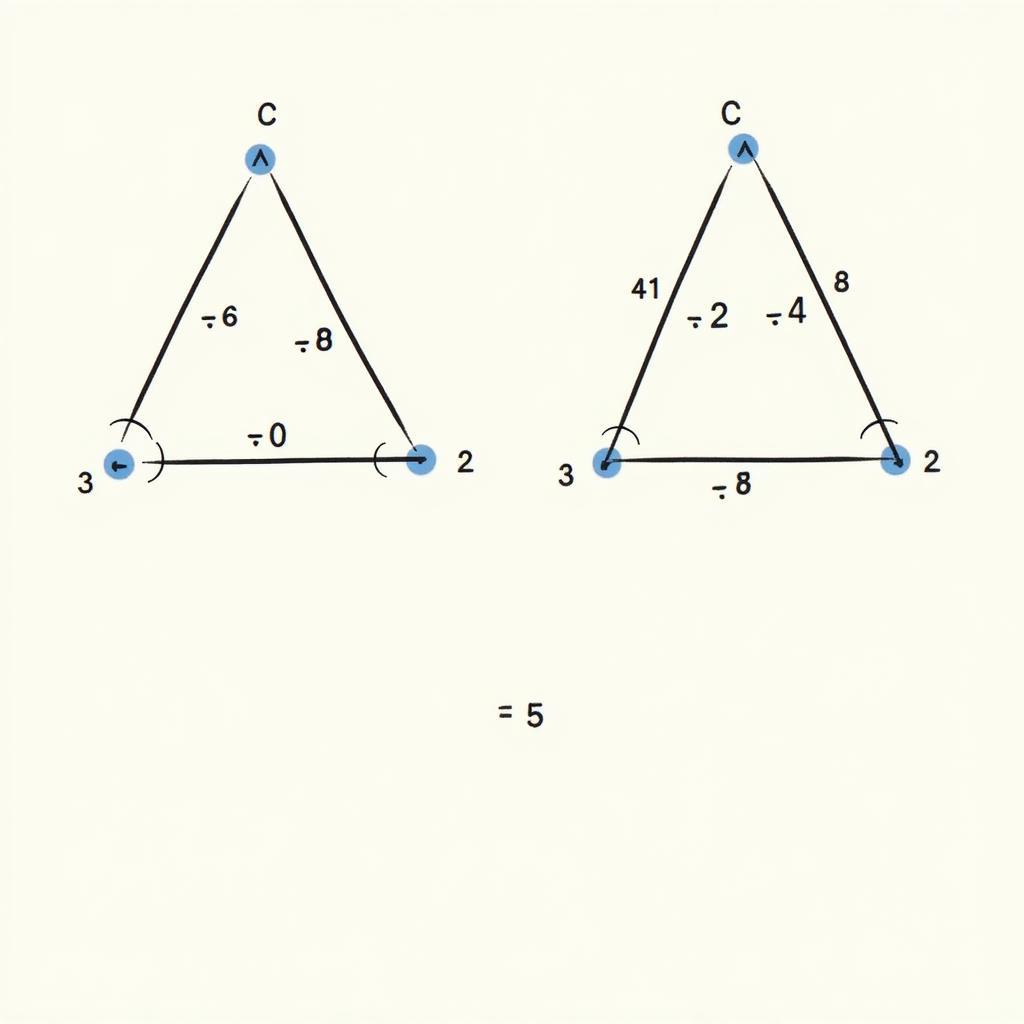 Điều kiện cần và đủ trường hợp cgc
Điều kiện cần và đủ trường hợp cgc
Ví dụ, nếu tam giác ABC và tam giác DEF có AB = DE, AC = DF, và góc BAC = góc EDF, thì tam giác ABC bằng tam giác DEF theo trường hợp c-g-c.
Ứng Dụng của Trường Hợp c-g-c trong Giải Toán
Trường hợp c-g-c không chỉ là một định lý toán học khô khan, mà còn là công cụ hữu ích để giải quyết nhiều bài toán hình học phức tạp. Nó giúp học sinh THPT Gia Định chứng minh các đoạn thẳng bằng nhau, góc bằng nhau, hay chứng minh hai tam giác bằng nhau để suy ra các tính chất khác.
“Việc nắm vững trường hợp c-g-c là chìa khóa để mở ra cánh cửa đến với thế giới hình học đầy thú vị,” Cô Nguyễn Thị A, giáo viên Toán tại THPT Gia Định, chia sẻ. bài giảng trường hợp đồng dạng thứ ba
Trường Hợp c-g-c trong Cuộc Sống
Ngoài ứng dụng trong toán học, trường hợp c-g-c còn có thể được áp dụng trong nhiều lĩnh vực khác của cuộc sống, ví dụ như trong xây dựng, kiến trúc, và thiết kế. Việc hiểu rõ về trường hợp này giúp các kỹ sư và kiến trúc sư thiết kế các công trình vững chắc và chính xác.
Trường hợp bằng nhau thứ hai: Những bài toán minh họa
bài văn viết về trường em
Dưới đây là một số bài toán minh họa về trường hợp bằng nhau thứ hai.
Kết Luận
Trường hợp 2 tam giác bằng nhau (c-g-c) là một kiến thức quan trọng trong hình học, có ứng dụng rộng rãi trong both học tập và thực tiễn. Hy vọng bài viết này đã giúp các bạn học sinh THPT Gia Định hiểu rõ hơn về trường hợp này. thời khóa biểu thpt
FAQ
- Trường hợp c-g-c là gì?
- Làm thế nào để chứng minh hai tam giác bằng nhau theo trường hợp c-g-c?
- Trường hợp c-g-c có ứng dụng gì trong thực tế?
- Phân biệt trường hợp c-g-c với các trường hợp bằng nhau khác của tam giác?
- Có những bài toán nào thường sử dụng trường hợp c-g-c để giải?
- Tài liệu nào giúp em ôn tập về trường hợp c-g-c?
- Trường hợp bằng nhau c-g-c có liên quan gì đến các kiến thức hình học khác? bài giảng trường hợp đồng dạng thứ nhất
Khi cần hỗ trợ hãy liên hệ Số Điện Thoại: 02223831609, Email: [email protected] Hoặc đến địa chỉ: Đ. Nguyễn Văn Cừ, Trang Hạ, Từ Sơn, Bắc Ninh, Việt Nam. Chúng tôi có đội ngũ chăm sóc khách hàng 24/7.