Khám Phá Các Trường Hợp Tam Giác Bằng Nhau Tại THPT Gia Định

Các Trường Hợp Tam Giác Bằng Nhau là một phần kiến thức nền tảng quan trọng trong hình học phẳng, giúp học sinh THPT Gia Định xây dựng tư duy logic và giải quyết các bài toán phức tạp. Hiểu rõ các trường hợp này không chỉ giúp các em đạt điểm cao trong các kỳ thi mà còn rèn luyện khả năng tư duy toán học, áp dụng vào thực tiễn. Ngay sau đoạn mở đầu này, chúng ta sẽ cùng nhau khám phá thế giới thú vị của các trường hợp tam giác bằng nhau. backdrop kỷ niệm ngày ra trường

Trường Hợp Cạnh – Cạnh – Cạnh (c.c.c)

Trường hợp c.c.c xác định rằng hai tam giác bằng nhau nếu ba cạnh của tam giác này lần lượt bằng ba cạnh của tam giác kia. Đây là trường hợp cơ bản và dễ hiểu nhất trong các trường hợp tam giác bằng nhau. Ví dụ, nếu tam giác ABC có AB = DE, BC = EF, và AC = DF, thì tam giác ABC bằng tam giác DEF.

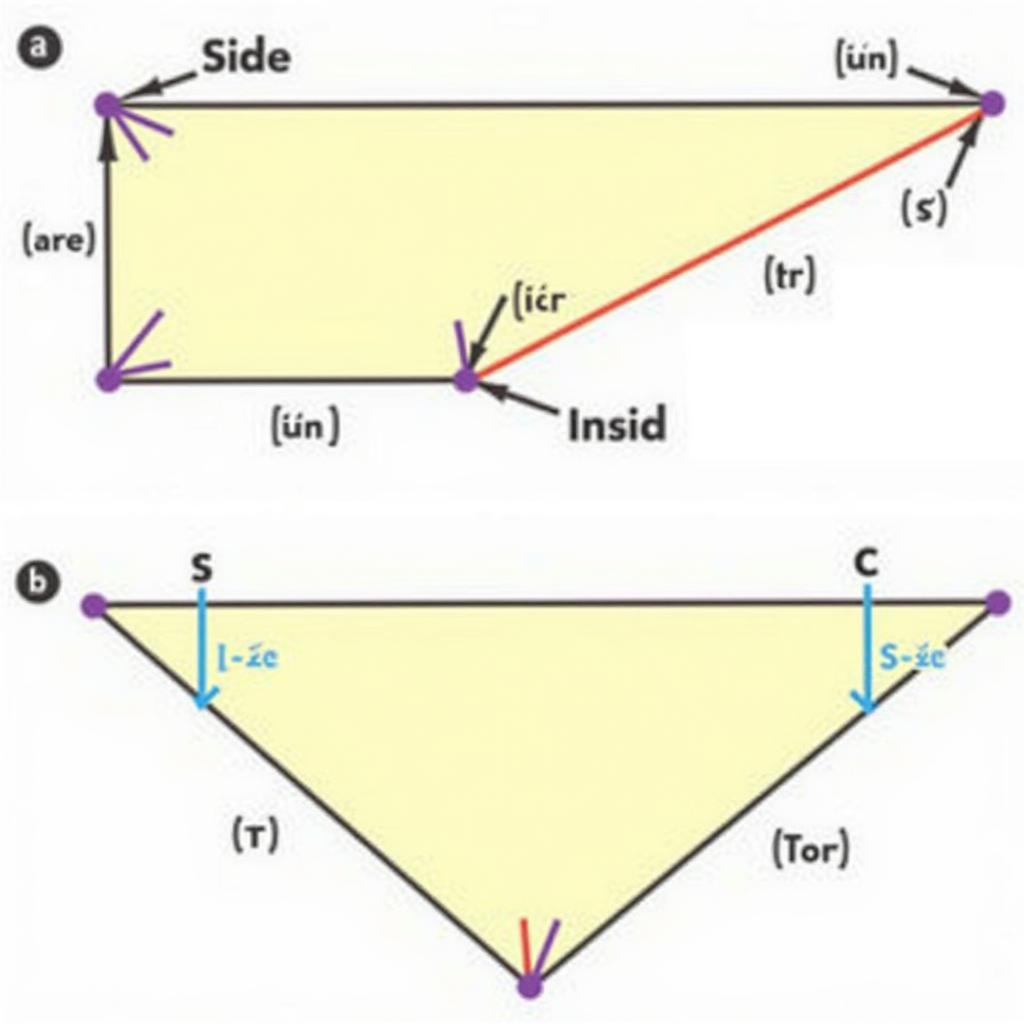Minh họa trường hợp cạnh cạnh cạnh

Trường Hợp Cạnh – Góc – Cạnh (c.g.c)

Hai tam giác được coi là bằng nhau theo trường hợp c.g.c nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia. Điều quan trọng cần nhớ là góc phải nằm giữa hai cạnh đã cho. Giả sử tam giác ABC có AB = DE, góc BAC = góc EDF, và AC = DF, thì ta có thể kết luận tam giác ABC bằng tam giác DEF.

Trường Hợp Góc – Cạnh – Góc (g.c.g)

Trường hợp g.c.g chỉ ra rằng hai tam giác bằng nhau nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia. Lưu ý rằng cạnh phải nằm kề với cả hai góc. Ví dụ, nếu tam giác ABC có góc BAC = góc EDF, AC = DF, và góc ACB = góc DFE, thì tam giác ABC bằng tam giác DEF.

Trường Hợp Cạnh Huyền – Góc Nhọn (ch.g.n) (Chỉ áp dụng cho tam giác vuông)

Trường hợp đặc biệt này chỉ áp dụng cho tam giác vuông. Hai tam giác vuông bằng nhau nếu cạnh huyền và một góc nhọn của tam giác này bằng cạnh huyền và một góc nhọn của tam giác kia. Ví dụ, nếu tam giác ABC và tam giác DEF là hai tam giác vuông tại A và D, và BC = EF (cạnh huyền), góc ABC = góc DEF (góc nhọn), thì tam giác ABC bằng tam giác DEF.

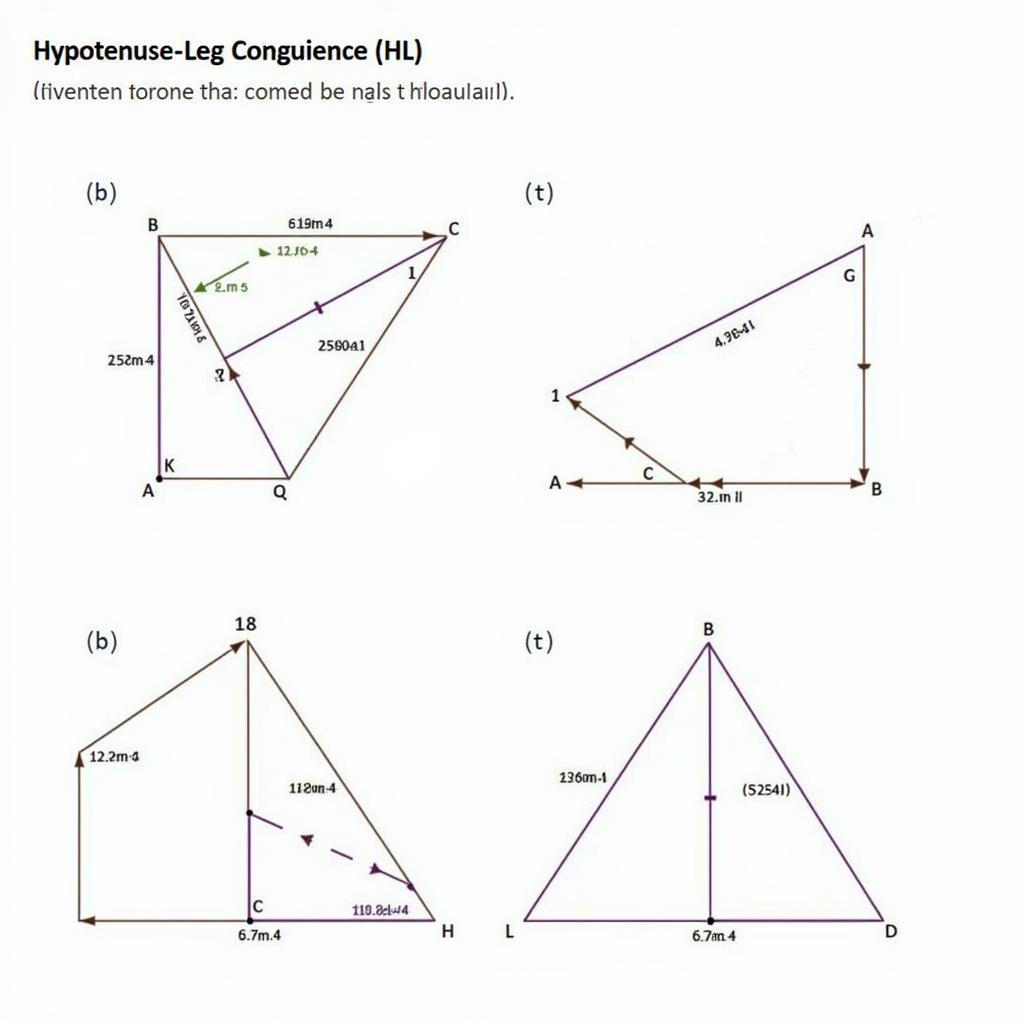Minh họa trường hợp cạnh huyền góc nhọn

Các Trường Hợp Tam Giác Bằng Nhau và Ứng Dụng Thực Tiễn

Việc nắm vững hướng dẫn ôn luyện thi thpt quốc gia về các trường hợp tam giác bằng nhau không chỉ giới hạn trong sách vở mà còn có thể áp dụng vào thực tiễn, ví dụ như trong việc đo đạc khoảng cách, xây dựng, thiết kế.

Theo thầy Nguyễn Văn A, giáo viên Toán tại THPT Gia Định: “Hiểu rõ các trường hợp tam giác bằng nhau là chìa khóa để giải quyết nhiều bài toán hình học phức tạp, đồng thời giúp học sinh phát triển tư duy logic và khả năng phân tích.”

Cô Trần Thị B, cũng là giáo viên Toán tại trường, bổ sung: “Việc vận dụng các trường hợp tam giác bằng nhau vào thực tiễn giúp học sinh nhìn thấy sự liên hệ giữa lý thuyết và thực hành, từ đó tăng hứng thú học tập.”

Kết Luận

Các trường hợp tam giác bằng nhau là kiến thức cốt lõi trong hình học. Hiểu rõ và vận dụng thành thạo các trường hợp c.c.c, c.g.c, g.c.g và ch.g.n sẽ giúp các em học sinh THPT Gia Định tự tin chinh phục mọi bài toán hình học. logo trường mầm non vector

FAQ

Có bao nhiêu trường hợp tam giác bằng nhau? (Có 4 trường hợp)
Trường hợp nào chỉ áp dụng cho tam giác vuông? (ch.g.n)
Trường hợp c.c.c là gì? (Ba cạnh bằng nhau)
Trường hợp g.c.g là gì? (Một cạnh và hai góc kề bằng nhau)
Làm thế nào để nhớ các trường hợp tam giác bằng nhau? (Học thuộc định nghĩa và làm bài tập thường xuyên)
Ứng dụng của các trường hợp tam giác bằng nhau trong thực tế là gì? (Đo đạc, xây dựng, thiết kế…)
Tại sao cần phải học các trường hợp tam giác bằng nhau? (Giúp giải quyết bài toán hình học và phát triển tư duy logic).

Tình huống thường gặp câu hỏi

Học sinh gặp khó khăn trong việc phân biệt giữa trường hợp c.g.c và g.c.g: Cần nhấn mạnh vị trí của góc so với hai cạnh. Trong c.g.c, góc nằm giữa hai cạnh, còn trong g.c.g, cạnh nằm giữa hai góc.
Học sinh quên trường hợp ch.g.n: Nhắc nhở học sinh đây là trường hợp đặc biệt chỉ áp dụng cho tam giác vuông.