Nguyên hàm tích phân là một trong những chủ đề quan trọng và thường xuyên xuất hiện trong đề thi THPT Quốc Gia môn Toán. Nắm vững kiến thức về nguyên hàm tích phân không chỉ giúp học sinh đạt điểm cao trong kỳ thi quan trọng này mà còn rèn luyện tư duy logic, khả năng phân tích và giải quyết vấn đề. Bài viết này sẽ cung cấp cho các em học sinh THPT Gia Định một cái nhìn tổng quan về nguyên hàm tích phân, cũng như những chiến lược ôn tập hiệu quả để chinh phục dạng bài này trong kỳ thi sắp tới. Ngay sau khi tốt nghiệp THPT, nhiều bạn học sinh lựa chọn trường cao đẳng thông tin hữu nghị việt hàn.
Tổng Quan về Nguyên Hàm và Tích Phân
Nguyên hàm và tích phân là hai khái niệm toán học có mối liên hệ mật thiết với nhau. Nguyên hàm của một hàm số f(x) là một hàm F(x) sao cho đạo hàm của F(x) bằng f(x). Tích phân xác định được hiểu là diện tích giới hạn bởi đồ thị hàm số, trục hoành và hai đường thẳng x = a và x = b. Tích phân xác định có thể được tính toán bằng cách sử dụng nguyên hàm của hàm số.
Các Dạng Bài Tập Nguyên Hàm Tích Phân Thường Gặp
Các dạng bài tập Nguyên Hàm Tích Phân Trong đề Thi Thpt Quốc Gia thường bao gồm: tính nguyên hàm của các hàm số cơ bản, tính tích phân xác định, ứng dụng tích phân để tính diện tích hình phẳng, thể tích khối tròn xoay, và giải các bài toán thực tế liên quan đến tích phân.
Tính Nguyên Hàm của các Hàm Số Cơ Bản
Đây là dạng bài cơ bản nhất, yêu cầu học sinh nắm vững công thức nguyên hàm của các hàm số thường gặp như hàm đa thức, hàm mũ, hàm lượng giác.
Tính Tích Phân Xác Định
Dạng bài này yêu cầu học sinh áp dụng công thức Newton-Leibniz để tính tích phân xác định. Việc nắm vững các phương pháp đổi biến số, tích phân từng phần là rất quan trọng để giải quyết các bài toán phức tạp hơn.
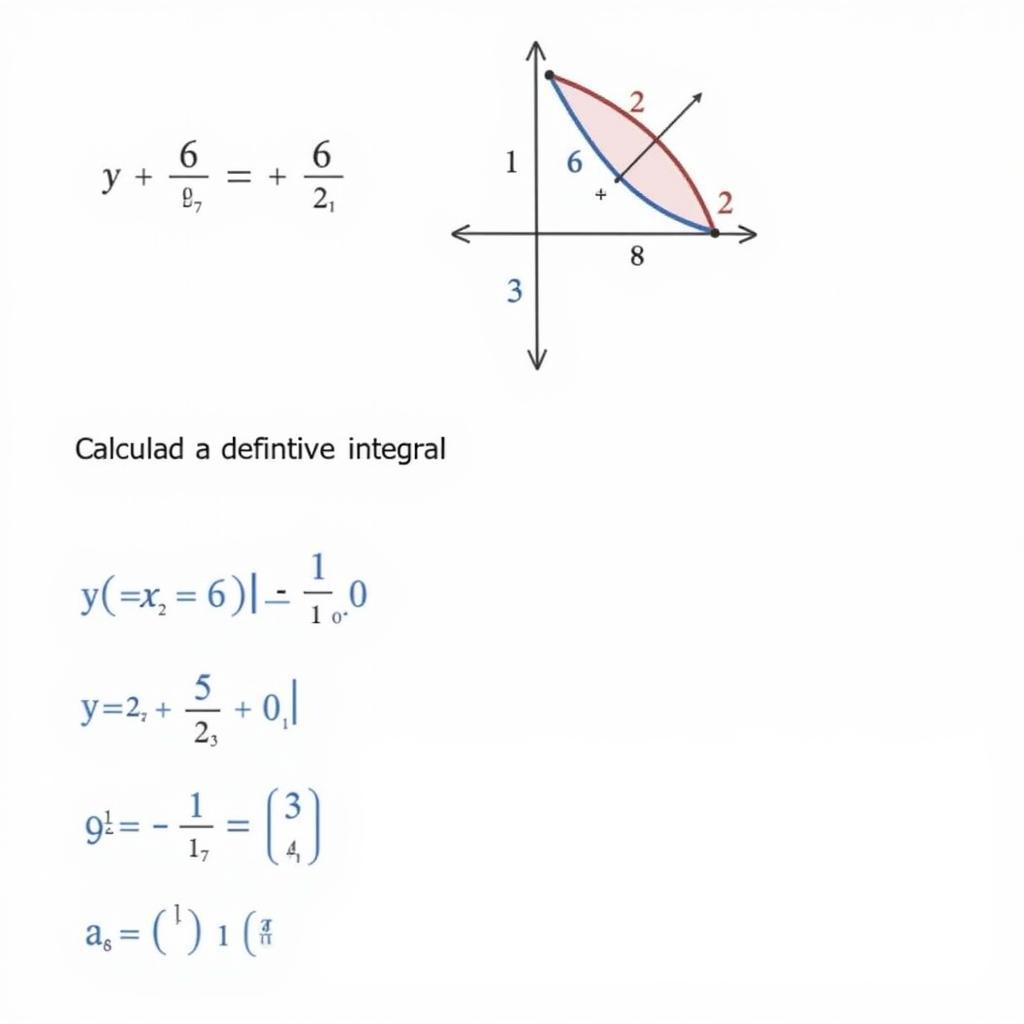 Tính tích phân xác định
Tính tích phân xác định
Ứng Dụng Tích Phân để Tính Diện Tích, Thể Tích
Đây là dạng bài nâng cao, yêu cầu học sinh vận dụng kiến thức tích phân để giải quyết các bài toán hình học. Học sinh cần nắm vững các công thức tính diện tích hình phẳng, thể tích khối tròn xoay. Có những trường hợp học sinh cần phải vẽ hình để xác định miền tích phân một cách chính xác.
Giải Bài Toán Thực Tế Liên Quan đến Tích Phân
Dạng bài này thường xuất hiện ở mức độ vận dụng cao, yêu cầu học sinh vận dụng kiến thức tích phân để giải quyết các bài toán thực tế trong các lĩnh vực như vật lý, kinh tế.
Phương Pháp Ôn Tập Hiệu Quả
Để ôn tập hiệu quả cho dạng bài nguyên hàm tích phân, học sinh cần nắm vững lý thuyết, làm nhiều bài tập từ cơ bản đến nâng cao, tham khảo các đề thi THPT Quốc Gia các năm trước. Ngoài ra, học sinh nên tìm hiểu thêm các tài liệu tham khảo, các bài giảng trực tuyến để củng cố kiến thức và nâng cao kỹ năng giải toán.
Ông Nguyễn Văn A, giáo viên Toán tại THPT Gia Định, chia sẻ: “Nguyên hàm tích phân là một chủ đề quan trọng trong chương trình Toán THPT. Học sinh cần ôn tập kỹ lưỡng, làm nhiều bài tập để nắm vững kiến thức và đạt kết quả tốt trong kỳ thi.”
Kết Luận
Nguyên hàm tích phân là một phần không thể thiếu trong đề thi THPT Quốc Gia. Bằng việc nắm vững kiến thức, luyện tập thường xuyên và áp dụng đúng phương pháp, học sinh hoàn toàn có thể chinh phục dạng bài này và đạt được kết quả mong muốn. Bạn có biết thpt hùng vương tphcm cũng là một trường THPT danh tiếng?
Bà Trần Thị B, cựu học sinh THPT Gia Định, chia sẻ: “Việc ôn tập kỹ lưỡng nguyên hàm tích phân đã giúp tôi đạt điểm cao trong kỳ thi THPT Quốc Gia. Tôi khuyên các em học sinh nên chú trọng vào việc luyện tập và làm nhiều bài tập để nắm vững kiến thức.”
FAQ
- Nguyên hàm là gì?
- Tích phân là gì?
- Làm thế nào để tính nguyên hàm của một hàm số?
- Làm thế nào để tính tích phân xác định?
- Ứng dụng của tích phân trong thực tế là gì?
- Làm thế nào để ôn tập hiệu quả cho dạng bài nguyên hàm tích phân?
- Tài liệu nào nên tham khảo để học tốt nguyên hàm tích phân?
Bạn đang tìm hiểu về ngành logistics nên học trường nào? Hãy tham khảo bài viết của chúng tôi.
Các tình huống thường gặp câu hỏi về nguyên hàm tích phân bao gồm việc xác định nguyên hàm của các hàm số khác nhau, tính toán tích phân xác định và ứng dụng của tích phân trong việc tính diện tích, thể tích và giải quyết các bài toán thực tế.
Bạn có thể tham khảo thêm các bài viết khác trên website của trường như diem thi tot nghiep thpt 2015 và trường chinh là ai.
Khi cần hỗ trợ hãy liên hệ Số Điện Thoại: 02223831609, Email: thptgiadinh@gmail.com Hoặc đến địa chỉ: Đ. Nguyễn Văn Cừ, Trang Hạ, Từ Sơn, Bắc Ninh, Việt Nam. Chúng tôi có đội ngũ chăm sóc khách hàng 24/7.